长方形被其内的一些线段分成了若干块 ,已知其中三块的面积分别是12、35、96,
阴影部分的面积是97。
解析:
因为长方形的面积等于△ABC与△ECD的面积和,所以△ABC与△ECD重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和。
如图: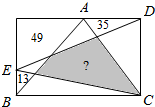
因为长方形的面积等于△ABC与△ECD的面积和,
所以△ABC与△ECD重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,
即:S=49+35+13=97。
故答案为:97。
长方形的性质为:
两条对角线相等;两条对角线互相平分;两组对边分别平行;两组对边分别相等;四个角都是直角;有2条对称轴(正方形有4条);具有不稳定性(易变形);长方形对角线长的平方为两边长平方的和;顺次连接矩形各边中点得到的四边形是菱形。