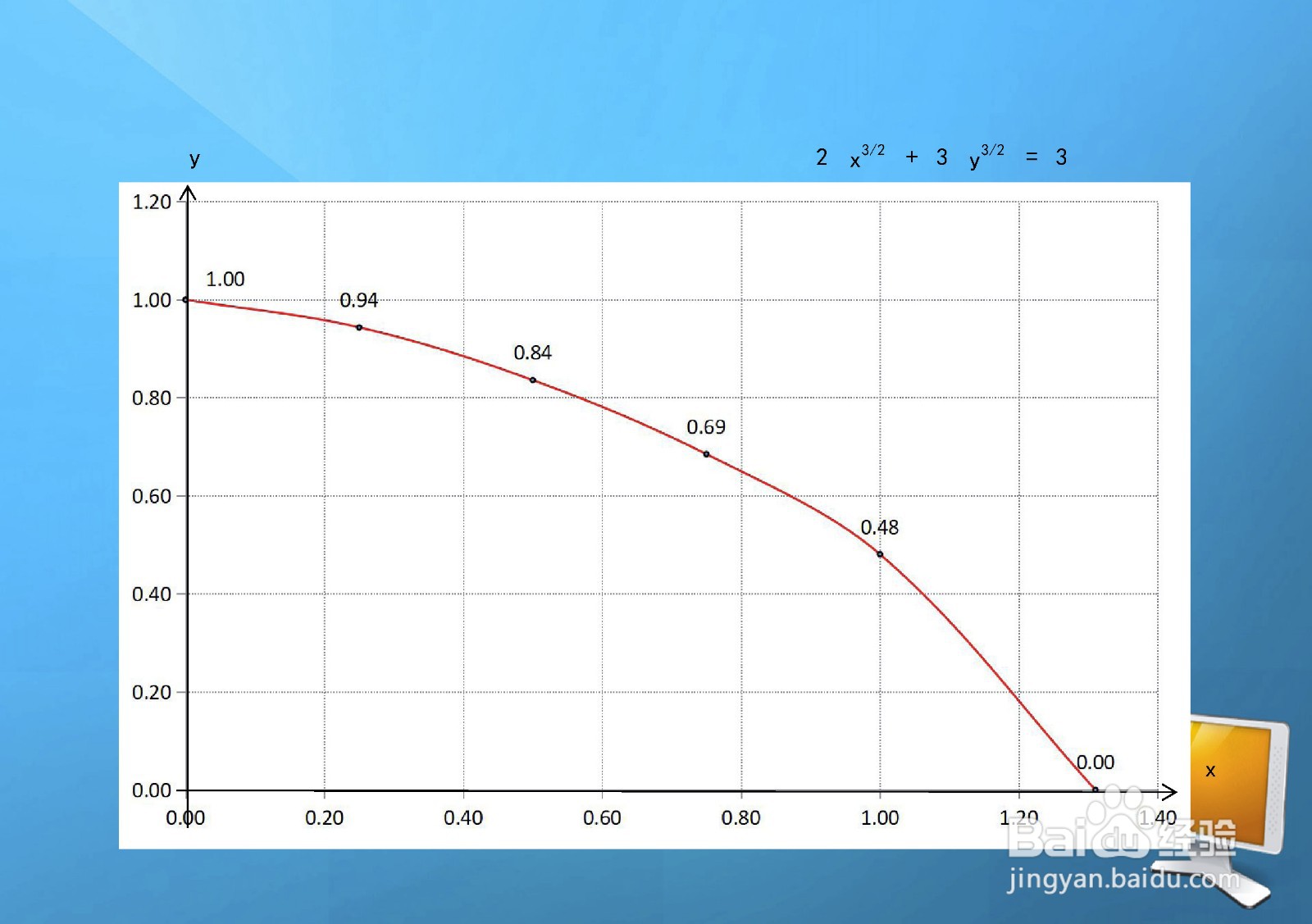
如何画隐函数2x^(3/2)+3y^(3/2)=3的图像

1、方程的定义域，主要是指方程习惯中自变量x的取值范围。本题是根据不等式性质来求解自变量x的取值范围。

3、判断函数的单调性，主要是求一阶导数，对方程两边同时对x求导，得到导数表达式。

6、 ※ . 函 数 的罕铞泱殳 凸 凹 性 ： 二阶导数，是原函数导数的导数，将原函数进行二次求导，本题是复合函数的二次求导，具体步骤如下： ∵ y' = - 2/3 ( y/x ) 1/2 . ∴ y〞 = -1/3 ( x/y ) -1/2 ( y - x y' ) y -2 = -1/3 ( y/x ) 1/2 [ y + 2/3 x ( x/y ) y/x ] y -2 = -1/9 ( y/x ) 1/2 ( 2 x 3/2 + 3 y 3/2 ) y -5/2 = - 1/3 x -1/2 y -2 即 y〞 < 0 。 则 ： 函 数 在 定 义 域 上 为 凸 函 数 。

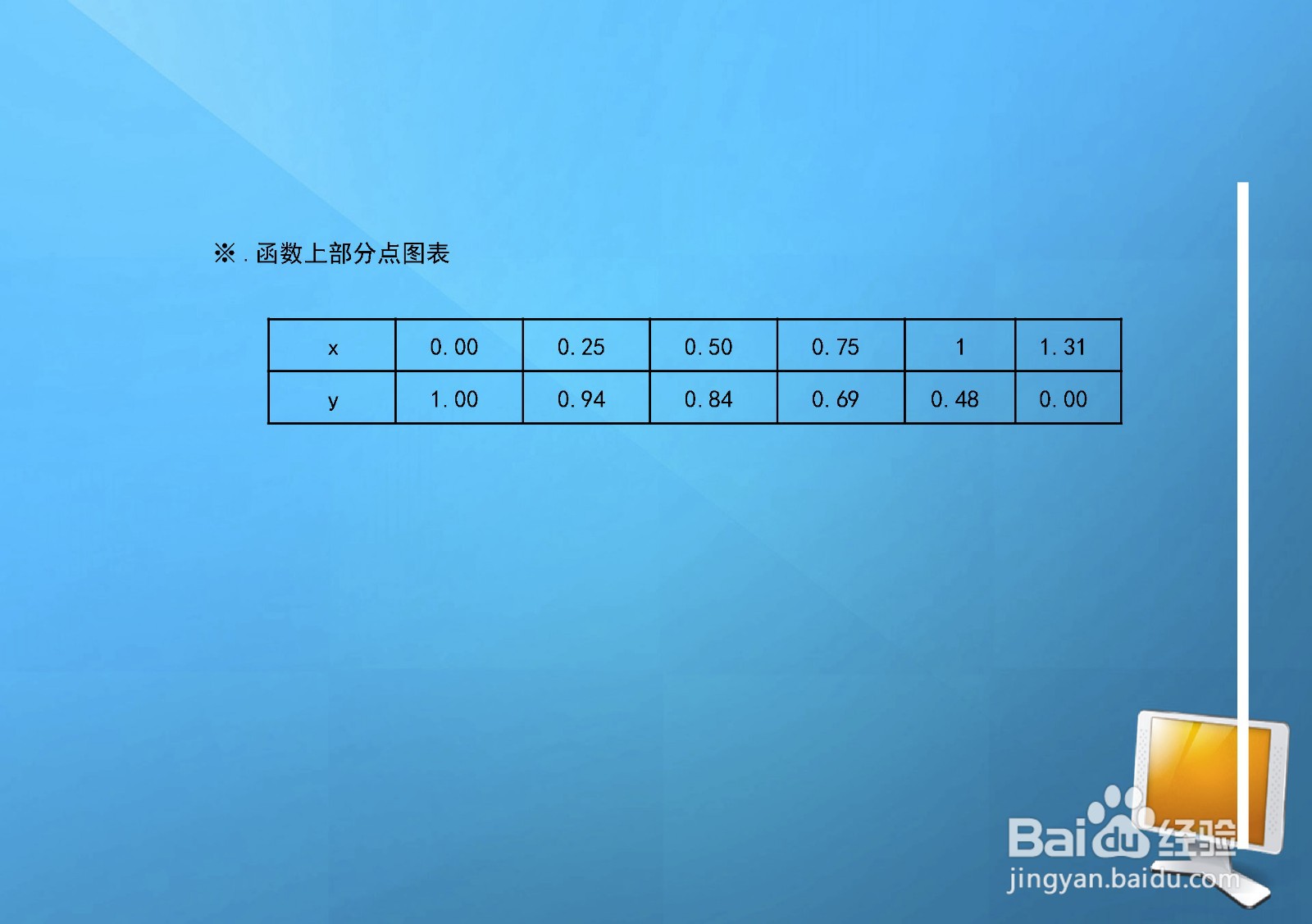
8、根据以上函数的单调性、凸凹性、极限等性质，曲线方程在直角坐标系的示意图如下。可见，整个函数图像在第一象限，成下降趋势，为递减函数，形如桥拱的一部分。