怎么在Matlab处理基于网络的插值
1、细化粗网格这个莲镘拎扇示例向您展示了如何为网格化数据集创建一个网格化中介,然后在一个更细的网格上进行插值。我们将首先定义一个为X和Y输入生成值的函数:generatevalues = @(X,Y)(3*(1-X).^2.*exp(-(X.^2) - (Y+1).^2) ... - 10*(X/5 - X.^3 - Y.^5).*exp(-X.^2-Y.^2) ... - 1/3*exp(-(X+1).^2 - Y.^2));
2、我们可以创建一个二维网格,然后将其传递给generatevalues函数,以在网格点处生成值。网格由一对网格矢量创建,如下所示:xgv = -1.5:0.25:1.5;ygv = -3:0.5:3;[X,Y] = ndgrid(xgv,ygv);
3、现在生成值数据:V = generatevalues(X,Y);
4、我们可以为这个数据集创建一个插值,支持网格内的插值。由于插值函数的行为类似于函数,我们将给它一个变量名“三次”选项指定三次插值。F = griddedInterpolant(X, Y, V, 'cubic')
5、按“Enter”键。得图1所示。
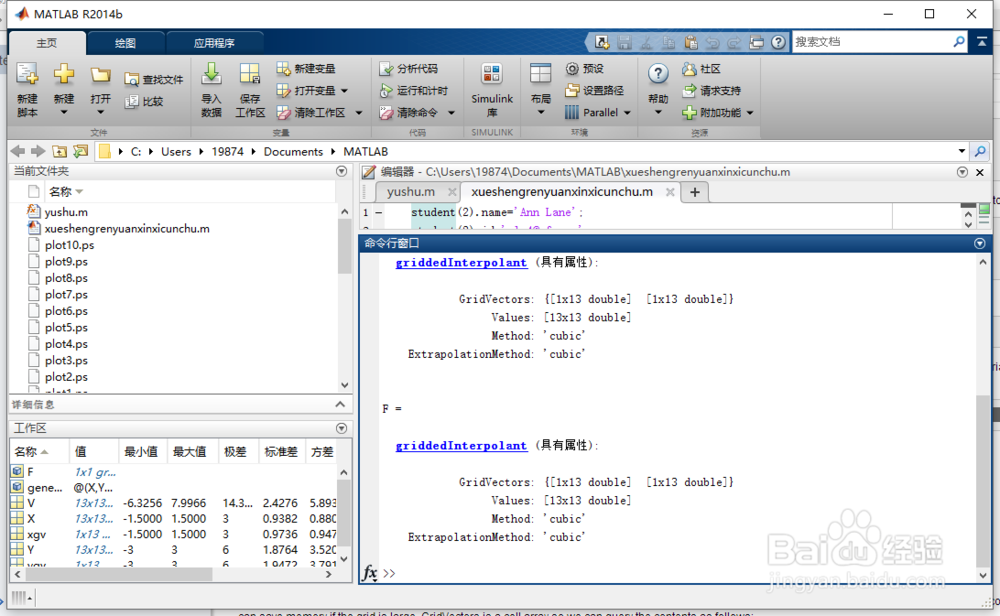
6、插值函数F有3个属性:GridVectors实际上是我们用来创建网格的向量xgv和ygv。内插器以紧凑的网格向量形式存储网格。如果网格很大,这可以节省内存。网格向量是一个单元格数组,所以我们可以如下查询内容:gridvectorprop = F.GridVectorsfirstgridvector = F.GridVectors{1}secondgridvector = F.GridVectors{2}
7、按“Enter”键。得图2所示。
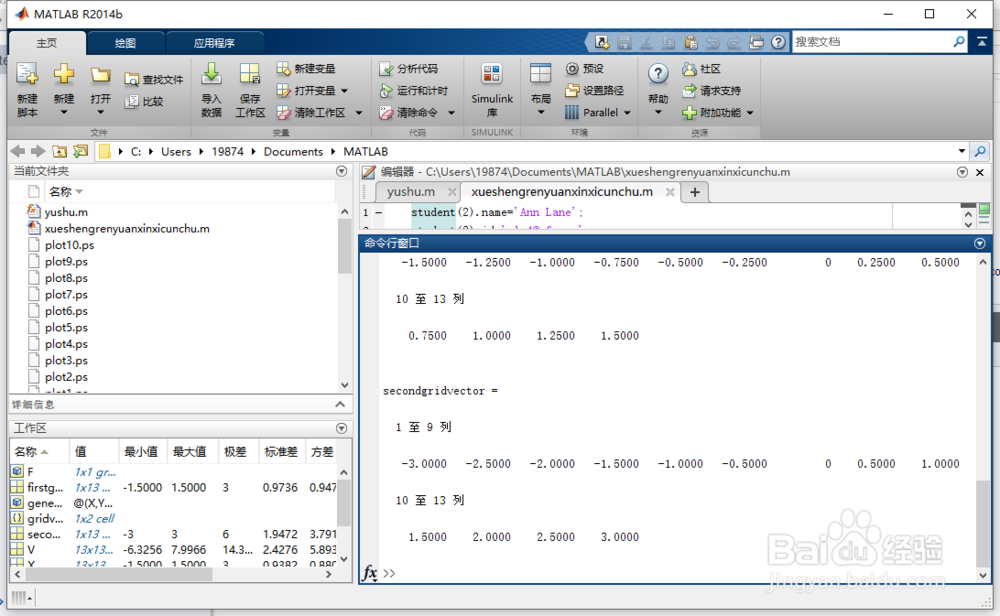
8、网格点的值存储在值数组中。您可以使用标准的MATLAB语法访问这些值以索引到数据中。例如,检查一个4乘5的间隔:first4x5values = F.Values(1:4, 1:5)
9、按“Enter”键。得图3所示。
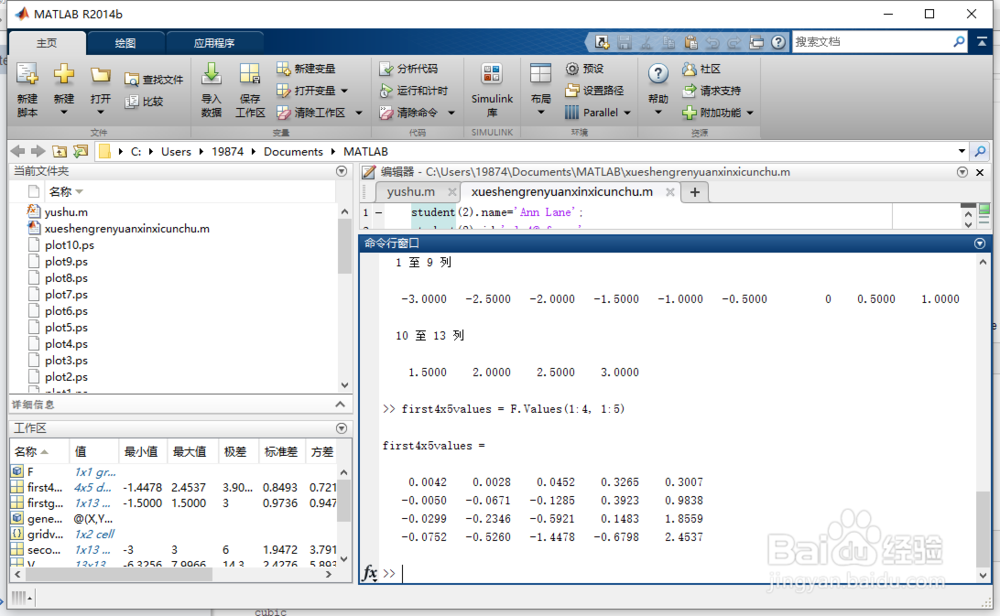
10、插值技术由方法的性质表示。我们选择了三次插值,我们的选择如下:theinterpolationmethod = F.Method
11、按“Enter”键。得图4所示。
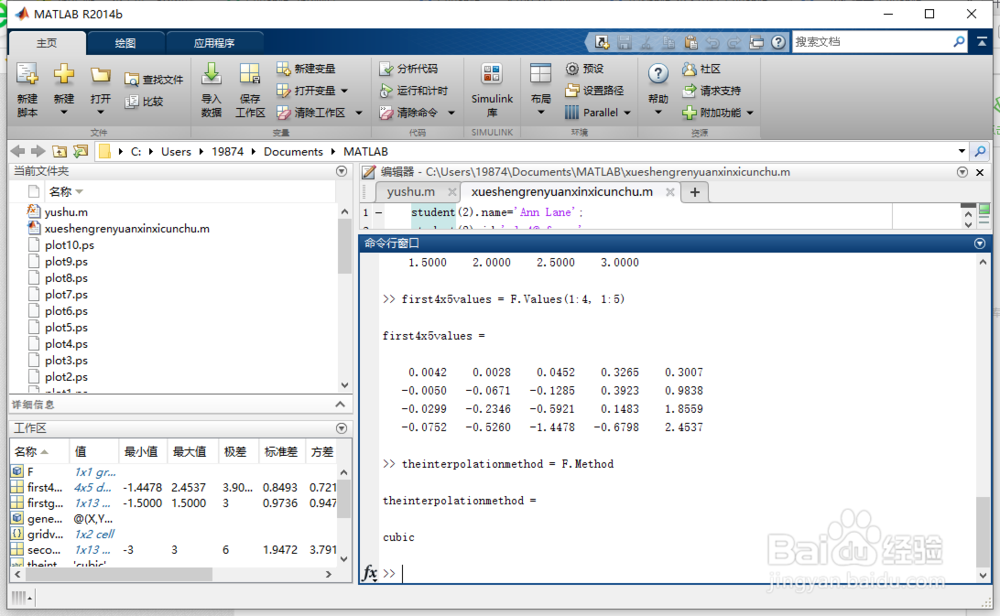
12、现在我们可以创建一个更好的网格,并使用插值计算这些点的值。我们将把这些点称为查询点(Xq,Yq),以便将它们与原始示例点区分开来。xqgv = -1.5:0.1:1.5;yqgv = -3:0.1:3;[Xq,Yq] = ndgrid(xqgv,yqgv);
13、现在,我们可以在精化网格上计算相应的值Vq(Xq,Yq)。因为我们给插值函数命名了F,所以调用语法是Vq = F(Xq, Yq);
14、我们现在可以生成一个图来与我们最初的粗图进行比较。figuresurf(X,Y,V)title(&垆杪屑丝#39;Gridded Data Set', 'fontweight','b');figuresurf(Xq, Yq, Vq);title('Gridded Data Set Refined using Cubic Interpolation', 'fontweight','b');
15、按“Enter”键。得图5、图6所示。
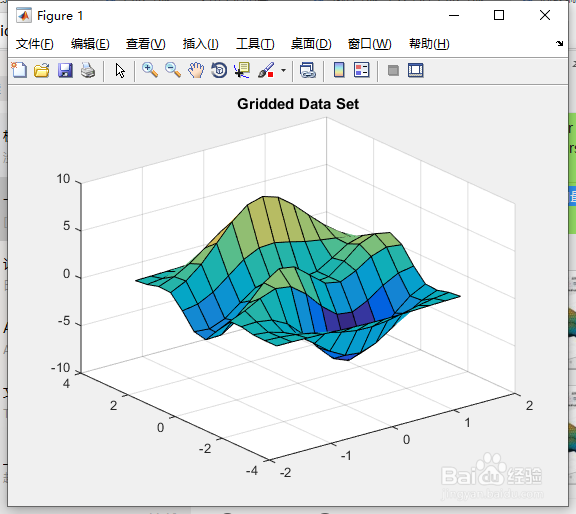
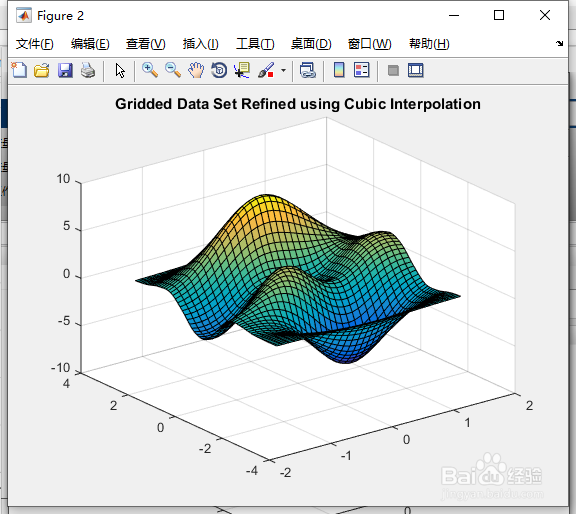
16、网格网格格式的数据插值网格中介类被设计用于处理符合NDGRID格式的网格数据。这提供了对一般N维网格的支持,包括可视为退化网格的一维网格。相比之下,MESHGRID格式只能支持二维和三维的网格。这两种网格类型都有相同的网格点坐标;不同的是坐标数组的格式。如果您希望使用MESHGRID数据创建一个网格化中介,您需要把数据转换为NDGRID格式。在二维中,这涉及如下面的示例所示的转换数组。xgv = -1.5:0.25:1.5;ygv = -3:0.5:3;[X,Y] = meshgrid(xgv,ygv);V = generatevalues(X,Y);
17、要将数据转换为NDGRID格式,请应用转置X = X';Y = Y';V = V';
18、我们现在可以创建一个插值函数F = griddedInterpolant(X, Y, V)
19、将三维网格网格数据转换为NDGRID格式需要转换三维数组的每个页面。这是通过使用PERMUTE函数来交换行(维度1)和列(维度2)来实现的。下面这个例子向你展示了:gv = -3多唉捋胝:3;[X,Y,Z] = meshgrid(gv);V = X.^2 + Y.^2 + Z.^2;P = [2 1 3];X = permute(X,P);Y = permute(Y,P);Z = permute(Z,P);V = permute(V,P);
20、我们现在可以创建一个插值函数F = griddedInterpolant(X, Y, Z, V)
21、同样,当使用MESHGRID查询插值函数时,可以通过转换为NDGRID格式来提高性能。例如,如果我们希望使用由查询点组成的MESHGRID来查询内插函数F(Xq,Yq,Zq),我们可以将数据转换为NDGRID格式,如下所示:[Xq, Yq, Zq] = meshgrid(0:0.5:2);Xq = permute(Xq,P);Yq = permute(Yq,P);Zq = permute(Zq,P);
22、现在的NDGRID格式(Xq、Yq、Zq)可以有效地进行查询。Vq = F(Xq,Yq,Zq);
23、一般尺寸的栅格网格介入类不限于2维和3维。您可以为1D、4D或更高版本创建内插函数。实际上,表示数据所需的内存可能是高维中的限制因素。根据网格点的数量和可用的计算能力,这种限制可能会影响到相对较低的维度(小于10)的使用。下面的例子说明了使用PCHIP插值方法的一维插值。X = 1:6;V = [16 18 21 17 15 12];F = griddedInterpolant(X,V,'pchip')
24、现在我们可以在更细的时间间隔内评估插值函数。Xq = 1:0.05:6;Vq = F(Xq);
25、用蓝色标出查询点,用红色标出插值结果:plot(X,V,'ob',Xq,Vq,'-r')title('1D Interpolation of a Data Set using the PCHIP Method', 'fontweight','b');
26、按“Enter”键。得图7所示。
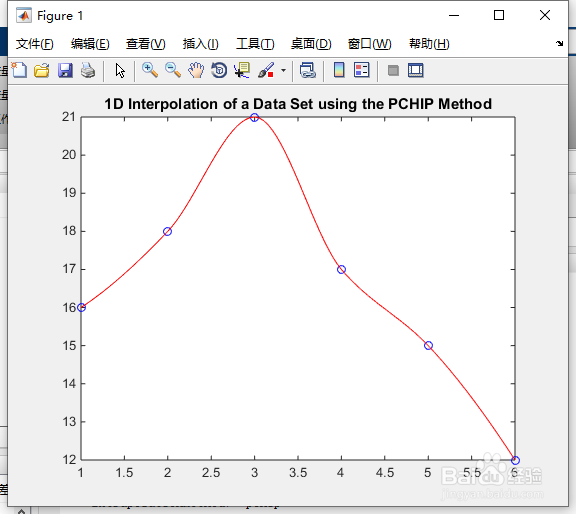
27、我们可以创建并查询一个4D插值函数,如下所示:[X1, X2, X3, X4] = ndgrid(1:6);V = X1.^2 + X2.^2 + X3.^2 + X4.^2;F = griddedInterpolant(X1,X2,X3,X4,V)
28、在单个4D点进行评估F(1.1,2.1,3.1,4.1)
29、比较(1.1)^2 + (2.1)^2 + (3.1)^2 + (4.1)^2
30、在4D点数组中求值Xq = 1 + 5*rand(5,4);Vq = F(Xq)
31、在每个网格点处具有多个值的插值网格在一些应用程序中,可能有多个与每个网格点相关联的撕良滤儆值,我们可能希望依次对每个值集进行插值。例如,如果我们有一个代表图像像素的网格,我们可能有三个与每个网格盼内溲铫点相关联的颜色强度(RGB)。有两种方法来插值这些数据。一种方法是为三个数据集中的每一个创建一个单独的内插器。另一种方法是创建一个内插函数并替换值。下面的示例演示了使用单个插值器替换值的方法。xgv = -1.5:0.25:1.5;ygv = -3:0.5:3;[X,Y] = ndgrid(xgv,ygv);% Create two distinct value sets for this gridV1 = X.^3 - 3*(Y.^2);V2 = 0.5*(X.^2) - 0.5*(Y.^2);% Now create an interpolant for the first value setF = griddedInterpolant(X,Y,V1, 'cubic')
32、我们可以在经过改进的网格上评估V1数据集,并绘制结果。xqgv = -1.5:0.1:1.5;yqgv = -3:0.1:3;[Xq,Yq] = ndgrid(旌忭檀挢xqgv,yqgv);Vq1 = F(Xq,Yq);figuresurf(Xq,Yq,Vq1);title('Cubic Interpolation of V1 Dataset', 'fontweight','b');
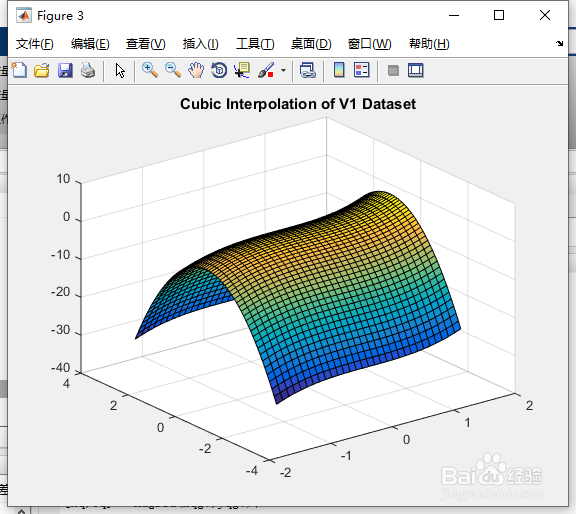
33、通过替换值数据,我们可以重用插值函数来插值第二个数据集。F.Values = V2
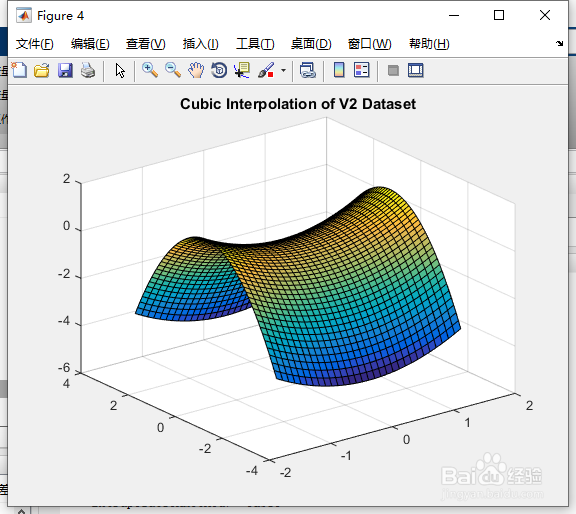
34、Vq2 = F(Xq,Yq);figuresurf(Xq,Yq,Vq2);title('Cubic Interpolation of V2 Dataset', 'fontweight','b');
35、按“Enter”键。得图8所示。
36、大型数据集网格中的中介类相对有效地处理大型数据集。这些数据集可以由外部生成的值网格组成,并导入到MAT讣嘬铮篌LAB中。例如,由外部源扫描的大的2D或3D图像。此外,这样的数据集可能没有明确定义的坐标数组网格。如果数据集是一个大的3D图像,网格坐标阵列的引入将使内存翻两番。griddedInterpolant类允许您从值网格中创建一个内插函数,然后根据数组的大小推导默认网格。这个默认网格是用网格向量来定义的——这是使用很少内存的网格的紧凑表示。为了说明这一点,我们可以使用PEAKS函数来生成一个值数组,然后为这个数据集创建一个插值函数,如下所示:V = peaks(10);F = griddedInterpolant(V,'cubic')
37、通过观察网格向量的性质,我们可以观察到矢量是由V阵的大小推导出来的。V是一个10x10的数组,相应的网格向量是1:10和1:10。firstgridvector = F.GridVectors{1}secondgridvector = F.GridVectors{2}
38、我们可以在一个改进过的网格上进行插值来提高分辨率,幸运的是,我们不需要创建一个完整的网格来实现这一点。我们可以使用一对网格向量进行计算,并将它们打包在花括号{}中,以表达这一意图。默认网格的缩放比例为1:10,因此我们将使用1:0.5:10对网格进行调整,以获得半间隔。相应的查询值矢量如下:Vq = F({1:0.5:10, 1:0.5:10});
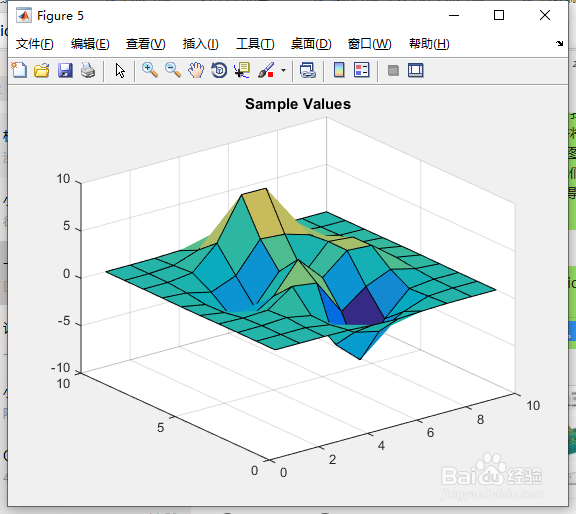
39、现在我们可以把结果并排标出来。figuresurf(V);title('Sample Values', 'fontweight','b');figuresurf(Vq);title('Cubic Interpolation using a Compact Grid', 'fontweight','b');
40、按“Enter”键。得图9、图10所示。
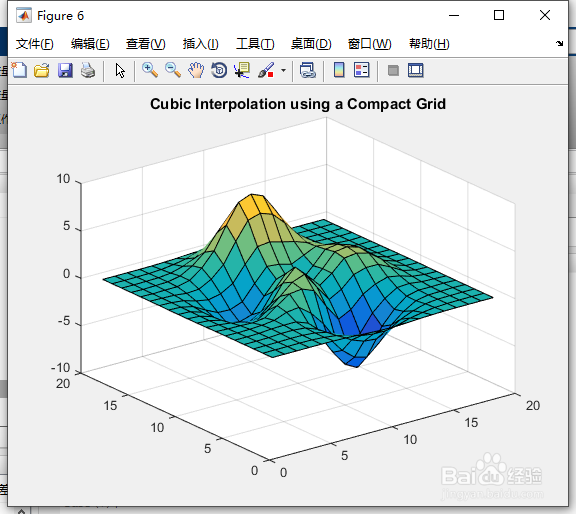
41、注意:当我们绘制表面时,SURF函数也使用默认网格来生成绘图。在第一个绘图中,值由一个10×10的数组表示,而第二个是20×20的数组表示。因此轴上有0-10和0-20的比例。在创建插值函数时,可以通过指定网格向量来复盖默认网格。例如,我们可以构造如下插值函数:F = griddedInterpolant({10:19, 20:29}, V,'cubic')
42、评价将遵循同样的尺度F(15,25)
43、默认的网格向量也可以被替换如下:F.GridVectors = {10:19, 20:29}
44、重复插值数据集在某些应用程序中,可能需要以重复的方式插入相同的数据集。与INTERP函数相比,网格中介类通常可以更有效地处理此场景。griddedInterpolant类能够重用在前一次查询中计算的数据,从而加快后续查询的计算速度。下面的示例显示了这一优势:样本数据集[X, Y, Z] = ndgrid(1:100);V = X.^2 + Y.^2 + Z.^2;
45、INTERPN的性能数据tic;for i = 1:1000 Xq = 100*rand(); Yq = 100*rand(); Zq = 100*rand(); Vq = interpn(X,Y,Z,V,Xq,Yq,Zq,'cubic');endinterpnTiming = toc
46、网格代理性能数据tic;F = griddedInterpolant(X,Y,Z,V, 'cubic');for i = 1:1000 Xq = 100*rand(); Yq = 100*rand(); Zq = 100*rand(); Vq = F(Xq,Yq,Zq);endgriddedInterpolantTiming = toc