图解九大基础排序算法
本篇经验将和大家介绍一下数据结构课程中常见的9大基础排序算法的算法描述、使用情况分析、参考代码等,希望对大家有所帮助。
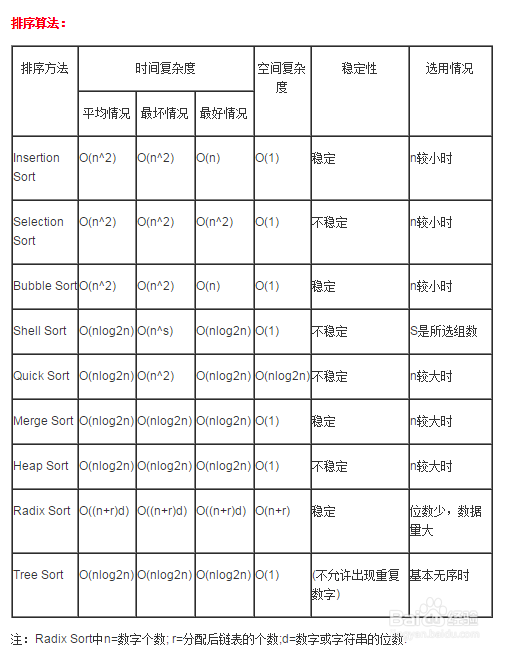
插入排序(Insertion Sort)
1、算法描述:Step1:将待排序数组分为有序和无序两组(初始情况下有序组为第一个元素)Step2:取出无序组第一个元素(First_unsorted)放入临时空间,将first_unsorted与有序组从最后一个元素开始进行比较,如果比有序组小,则将有序组中的该元素向后移一位,直到找到第一个比first_unsorted小的时候,将first_unsorted放入。至此,有序组++,无序组--。Step3:重复step2,直到无序组数量为0.算法结束。
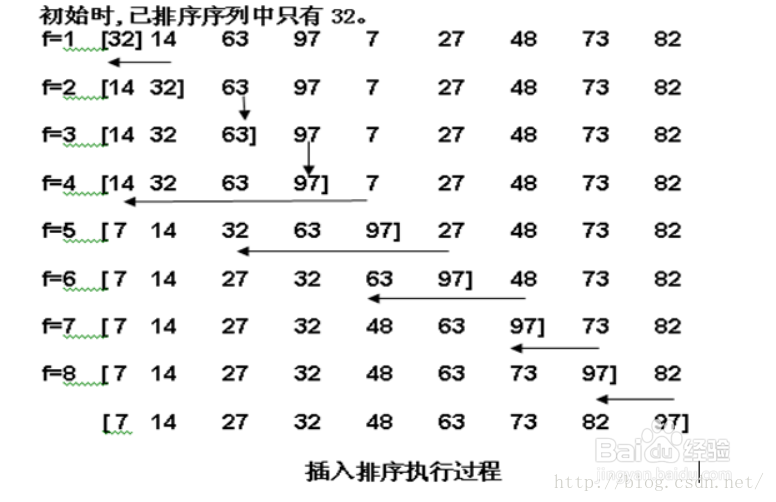
2、适用情况分析:稳定数组,链表均可实现空间复杂度O(1)时间复杂度O(n2)最差情况:反序,需要移动n*(n-1)/2个元素最好情况:正序,不需要移动元素数据量较小,较有序的情况下性能较好
3、(顺序版本)参考代码如下图所示:
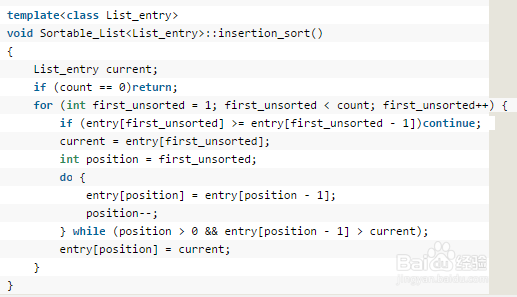
4、链式版本代码如下图所示:

选择排序(selection Sort)
1、算法描述:Step1:将待排序数组分为有序和无序两组(初始情况下有序组为空)Step2:从左向右扫描无序组,找出最小的元素,将其放置在无序组的第一个位置。至此有序组++,无序组--;Step3:重复Step2,直至无序组只剩下一个元素。算法结束。
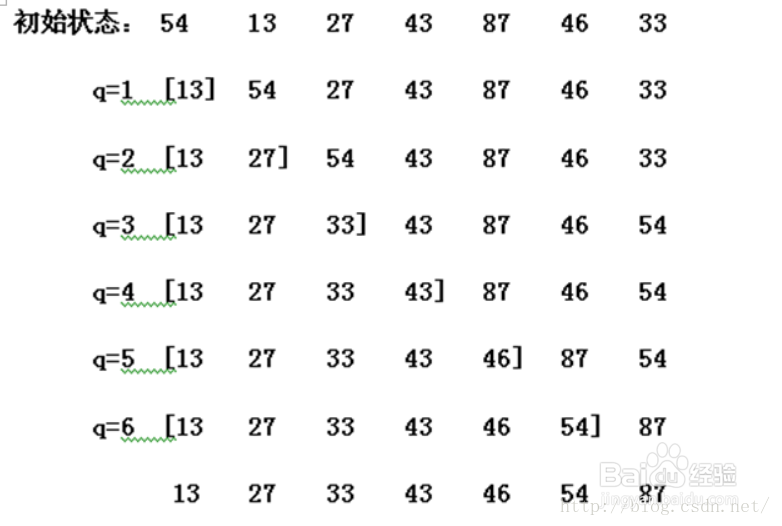
2、适用情苄念上妒况分析:不稳定数组,链表均可实现空间复杂度:O(1)时间复杂度:O(n2) 最坏情况:O(n2) 第一个元素为最大元素,其余元素正序,需要交换n-1个元素(如:4 3 2 1)最好情况:O(n2) 正序,不需要交换元素选择排序的最坏情况和最好情况下的实际没有太大区别。即选择排序对于原始记录的顺序不敏感。
3、参考代码如下图所示:

冒泡排序(Bubble Sort)
1、算法描述:Step1:比较相邻的元素。如果第一个比第二个大,就交换他们两个Step2:对每一对元素均进行此操作,经过一轮后最大的元素应位于最后一位Step3:从第一个元素重复进行前两步,每一轮最后一个元素都不参与比较,进行n轮算法结束。
2、适用情况分析:稳定大部分采取顺序,链式也可实现空间复杂度O(1)时间复杂度O(n2)数据顺序对算法影响不大
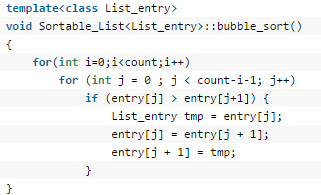
3、参考代码如下图所示:
希尔排序(Shell Sort)---插入排序的优化
1、算法描述:Step1:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序。Step2:依关骇脘骱次缩减增量再进行排序。Step3:待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。算法结束。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序相较于前几种方法有较大的提升。

2、适用情苄念上妒况分析:不稳定采取顺序实现,对下标敏感空间复杂度O(1)时间复杂度O(nlogn)步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。Donald Shell 最初建议步长选择为N/2并且对步长取半直到步长达到1已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,...)
3、参考代码如下图所示:
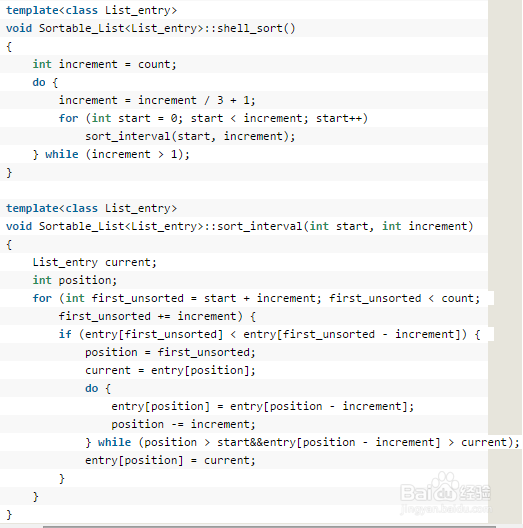
4、在网络上看到了简化版本的shell sort,也可作参考,如下图所示:

快速排序(Quick Sort)
1、算法描述:Step1:在待排序列中选取一个轴点(pivot),通常选取中间点Step2:将轴点与其他元素进行比较,将比轴点小的元素聚刁擞蛔放在轴点之前,比轴点大的元素放在轴点之后。至此,pivot已被排好序Step3:对0-(pivot-1)和(pivot+1)-n分别递归进行上述两步。算法结束。

2、适用情况分析:不稳定。顺序实现空间复杂度:O(1)时间复杂度:O(nlog2n)最坏情况:O(n2)要排序数组基本有序,基准值每次取最大(最小)元素,退化为冒泡。最好情况:O(nlog2n) 基准值两边元素个数基本相同.
3、参考代码如下图所示:

归并排序(Merge Sort)
1、算法描述:Step1:把待排序的列表划分为分成近似相等的两部分Step2:分别将两个子列表排序(递归进行)Step3:然后再合并成一个完整的列表算法结束。
2、使用情况分析:稳定链式实现空间复杂度:O(n)时间复杂度:O(nlog2n)最坏情况:O(nlog2n)最好情况:O(nlog2n)
3、参考代码如下图所示:

堆排序(Heap Sort)
1、算法描述: 堆的定义:堆是一棵完全二叉树或者是近似完全二叉树。根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最小者的堆称为小根堆,又称最小堆。根结盼内溲铫点(亦称为堆顶)的关键字是堆里所有结点关键字中最大者,称为大根堆,又称最大堆。Step1:建堆,序列分成无序和有序两组(初始有序为0)Step2:取出堆顶最大的元素,与待排序列的最后一个元素作交换,至此,无序组--,有序组++,并对无序组进行堆调整Step3:重复上述步骤,直至无序组仅剩一个元素算法结束。
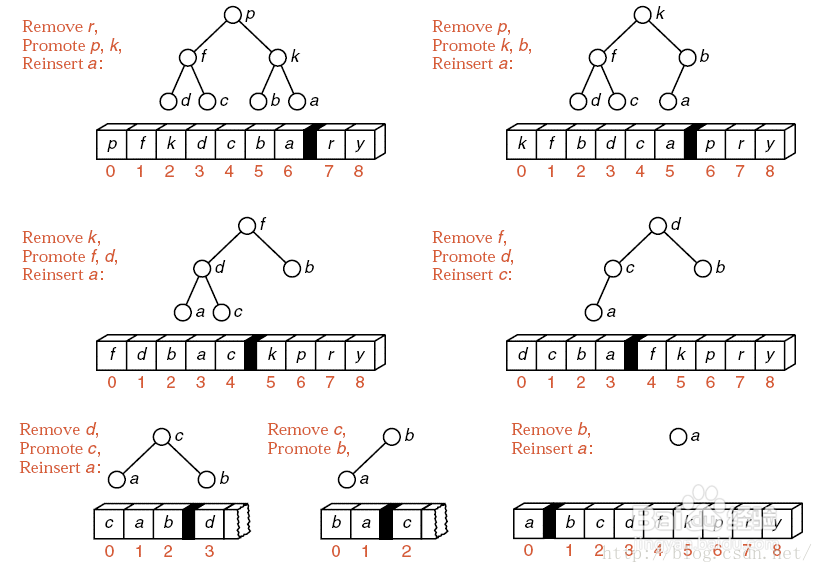
2、使用情况分析:不稳定顺序结构实现时间复杂度:o(nlogn)空间复杂度:o(1)由于建初始堆所需的比较次数较多,不建议在数据量小的情况下使用
3、代码如下图所示:

基数排序(Radix Sort)
1、算法描述:LSD:Step1:将待排序的元素按照最后一位进行分桶操作(桶按照最后一位排序从大到小)Step2:按顺序将各个桶中的数据连接起来,形成新的又挨喁钒序列Step3:依次对新序列的倒数第二位至第一位进行上述两步操作算法结束MSD:Step1:将待排序的元素按照最高位进行分桶操作Step2:对每个桶的按照第二位进行再次分桶(递归进行)Step3:进行至最后一位分桶操作完成后,对每个桶进行合并操作,得到有序序列算法结束
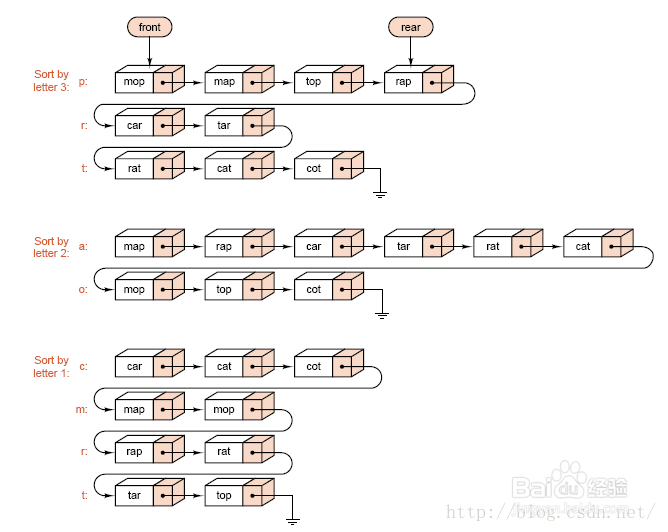
2、使用情况分析:稳定链式实现时间复杂度:假设在基数排序中,r为基数,d为位数。则基数排序的时间复杂度为O(d(n+r))空间复杂度:在基数排序过程中,对于任何位数上的基数进行“装桶”操作时,都需要n+r个临时空间数据量大时有明显优势,通常使用LSD法
3、MSD参考代码如下图所示:
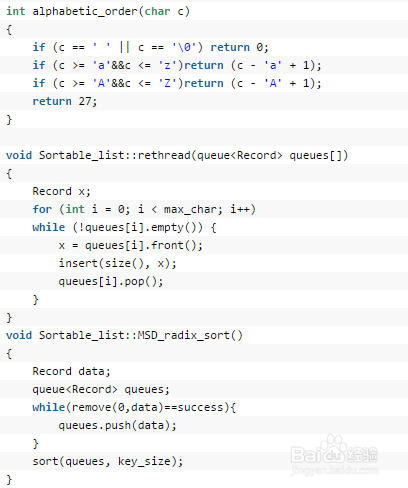
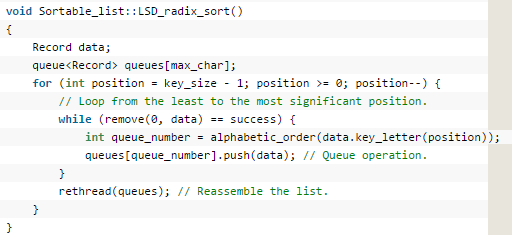
4、LSD参考代码如下图所示:
树排序(Tree Sort)
1、算法描述:对于一棵二叉查找树,中序遍历的序列即为有序序列。因此,二叉查找树的插入过程也可以看成是排序的过程。即Step1:将无序序列逐一插入二叉排序树。Step2:对二叉排序树进行中序遍历算法结束
2、适用情况分析:不稳定链式实现时间复杂度:o(nlogn)空间复杂度:o(1)Tree sort比较适合于无序的序列,对于基本有序的序列效率较低
3、参考代码如下图所示:
