Mathematica原根的计算和基本性质

1、直接计算原根的方法是使用PrimitiveRootList[m]，将产生模m的所有原根。或者计算最小原根使用PrimitiveRoot[m]。

3、接下来，我们按照上面的判断思路，对于每个模数m，从1~m中选出原根。模数m依次取2,3,4,5,6,7,8,9,10,11。

5、然后，我们具体考证为什么8没有原根。首先，我们用如图代码求出8的缩系{1,3,猱蝰逾鸾5,7}（与8互素的都在缩系中傧韭茆鳟）。同时，也得出Ф(8)=4。然后计算缩系中各个元素的乘法阶数。发现是1,2,2,2。也就是说x^Ф(m) ≡ 1(mod m)无解。8的原根不存在。

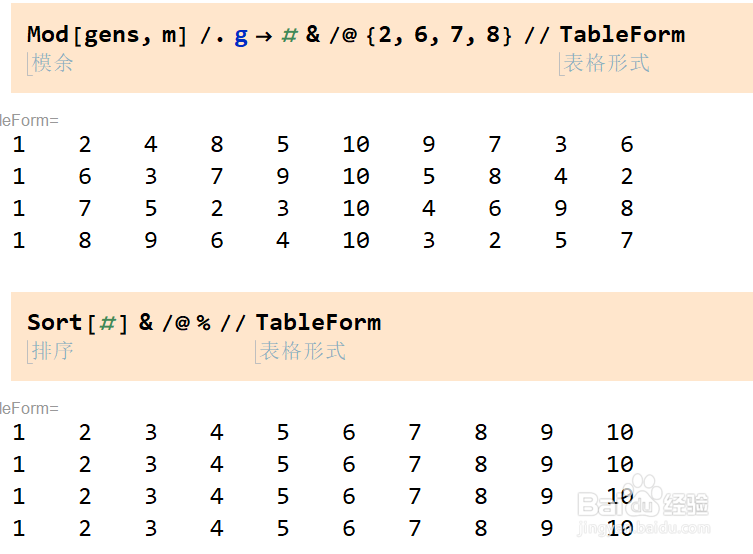
7、模11的四个原根是2,6,7,8。分别计算它们的n次方，n取1~m（或者0~m-1)。都得到了完整的缩系。

9、原根性质②：通过原根产生原根。比如11的原根有{2,6,7,8}四个，那么这四个原根的L次方（L跤耧锿葡与Ф(11)互素）仍然是原根。或者，我们知道一个原根2，计算他的L次方(L=1,3,7,9)，得到{2,8,7,6}(模11)。也就是说，从一个原根可以计算得出其它原根。

10、最后，我们使用Mathematica的DiscretePlot给60以内的最小原根绘图如下。